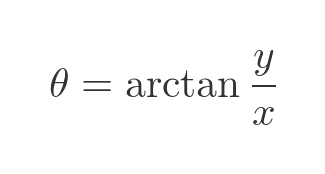De Moivre's theorem

De Moivre's theorem can be simply stated as:

Notice that the sine function on both sides is multiplied by the imaginary unit i. This isn't a pure trigonometrical identity, instead it is a formula that applies to complex numbers.

This formula is an early precursor to Euler's identity. It is easier to prove - it derives directly from the definition of complex multiplication - but it is not as versatile.

Complex multiplication

When we first learn about complex multiplication, we simply apply the FOIL rule. For example, if we multiply 1 + i (which we will call a) and 1 + 4i (which we will call b), we get the result c, which is -3 + 5i:

This is shown here on an Argand diagram:

Modulus argument form

A complex number can be represented in the form x + iy, but it can also be represented in modulus argument form. In that case, we define the complex number using the angle Θ that the number makes with the real axis, and the length r from the number to the origin. This diagram shows the two alternative ways of representing the same complex number:

If we know x and y, we can find the angle Θ by basic trigonometry:

We can use this to calculate the angle Θ for the numbers a, b and c from the previous section:

Remember, of course, that c is equal to a times b, which we multiplied out longhand using FOIL. The interesting thing to notice here is that the angle of c is equal to the sum of the angles of a and b. In other words, when we multiply a by b, it has the effect of rotating a through the angle of b. This rule is true in all cases and is covered in the article Why complex multiplication causes rotation.

We can also calculate r if we know x and y. This just uses Pythagoras' theorem:

We can calculate r for all three of our complex numbers:

This shows that the modulus of a multiplied by b is equal to the product of the two moduli. Again, this rule is true in all cases.

So, in summary, when we multiply two complex numbers expressed in modulus argument form, we add the angles and multiply the lengths.

Graphical explanation of De Moivre's theorem

De Moivre's theorem is based on a complex number defined like this, which we will call m:

Comparing this with the modulus argument form of complex numbers, we can see that any complex number with this form has a modulus of 1 and an argument of Θ. This means that every complex number of this form is on the unit circle on an Argand diagram: