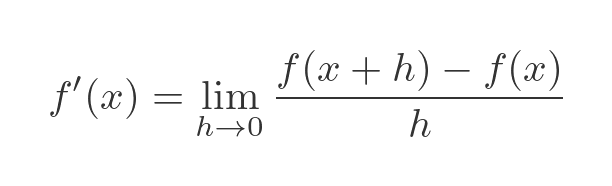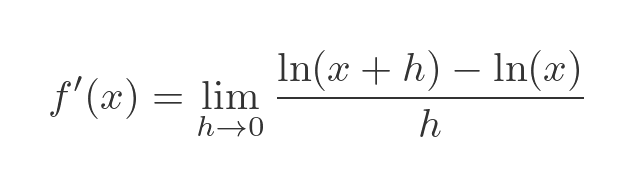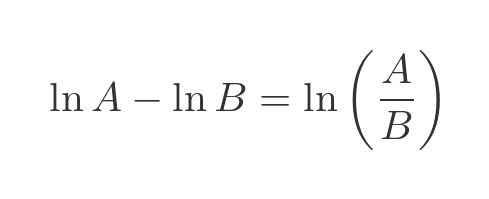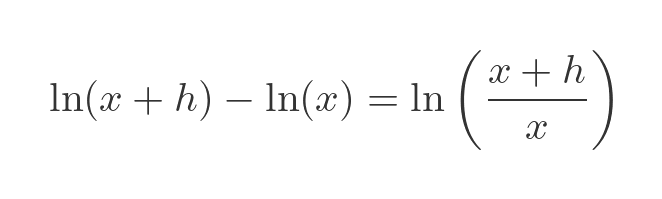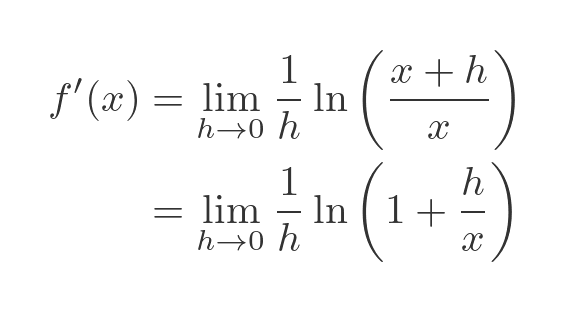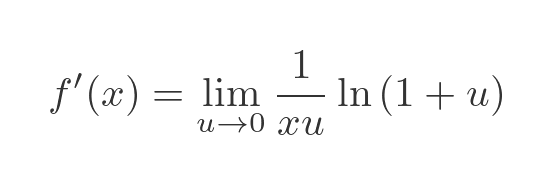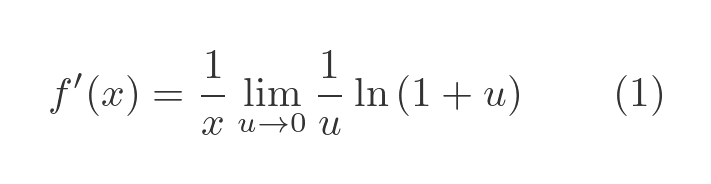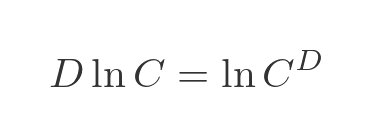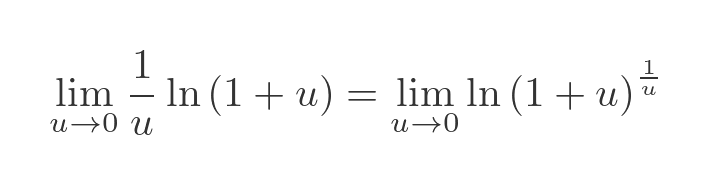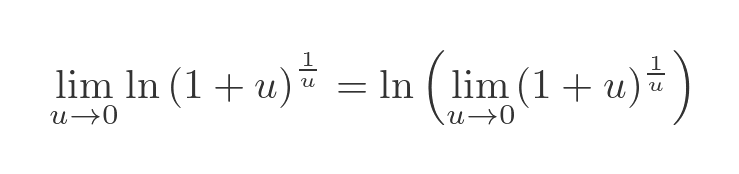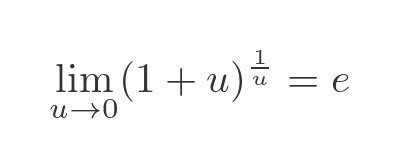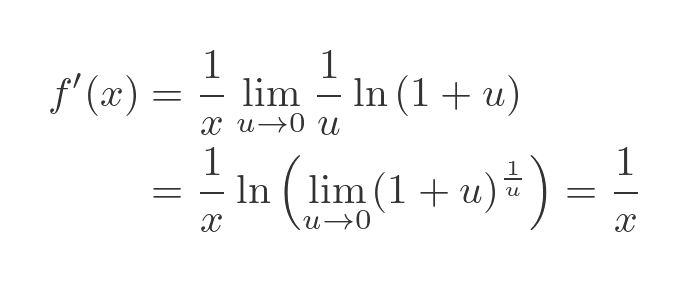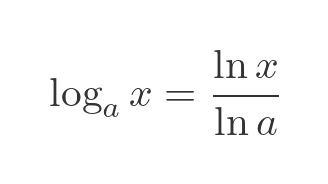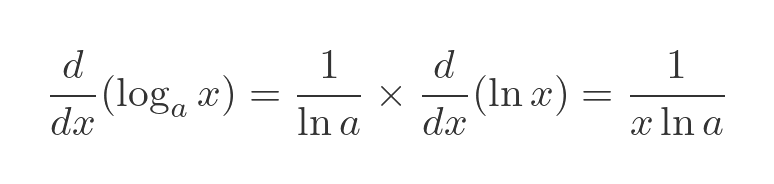Derivative of ln x from first principles

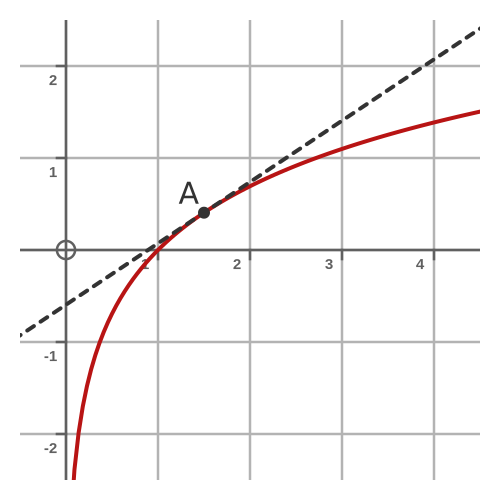
In this article, we will find the derivative of the natural logarithm function, ln(x). The natural logarithm, of course, is the logarithm using base e, where e is Euler’s number. Here is a graph of the function:

The ln function is defined for all x > 0, and is differentiable over that entire range. The graph shows the slope of the curve at point A.

We will see how to find the derivative from first principles. It is also possible to use the inverse function rule to find the derivative, because ln is the inverse of the exponential function. This article on the inverse function rule uses the ln function as a worked example.

We will also extend this to cover logarithms using any base.

If you find this article interesting, I also have a book on Calculus available.

Derivative of ln x from first principles

We can find the derivative of some function f(x) using the general first principles formula:

If you want to learn more about this technique, see the linked article. The first step is to substitute the general formula f(x) with pur specific formula ln(x)

Here we are subtracting two logarithms, which, of course, is equivalent to the logarithm of the quotient of the two terms:

So:

Putting this back into the main equation gives us:

In the second line, we have simply rearranged the term in the brackets.

There are a couple of important things we can observe about x. First, we are calculating f’(x) for some particular value of x. This means that when we calculate the limit, x is effectively a constant. For example, if we wanted to find f’(2), we would calculate the limit taking x as the fixed value 2.

The second thing to remember is that, because we are dealing with the ln function, we know that x will always be positive. In particular, it cannot be zero.

So we can make the following variable substitution, where u is simply h divided by the positive constant x:

Let’s make the substitution. Notice that because u is just h divided by a positive constant, it follows that as h tends to zero, then u tends to zero:

Finally, because x is a constant as far as the limit is concerned, we can take it outside the limit:

Now the limit itself only depends on u, so the limit will be a constant. But what is that constant? Well, we can use another logarithm law:

Applying this to the term inside the limit gives us:

Now the term inside the limit is the natural log of an expression that depends only on u. So the limit will be the log of whatever that expression tends to as u tends to zero. This means that we can move the limit to inside the log function:

Now you might recognise this famous limit (if not, it is covered here). The limit evaluates to Euler’s number, e:

So we can find the natural log of this limit. Since e is the base of natural logarithms, the log of e is simply 1:

So, the entire limit expression evaluates to 1. Putting this back into equation (1) gives the final result:

This agrees with the result obtained using the inverse function rule, shown here.

Differentiating logarithms using different bases

We can easily differentiate logarithms using other bases (for example, 10 and 2 are commonly used).

In general, any logarithm using base a can be expressed in terms of natural logarithms (ie base e) using a simple scaling factor based on the natural log of a:

Differentiating this gives: