Factors of a prime squared minus one — a surprising result?

This is a past question from the Cambridge University Maths entrance interview. It is an interesting open-ended question with quite a surprising result. Consider the following value n:

Where p is a prime number greater than 3.

The question is: what can you say about the prime factors of n?

Think about it before looking at the answer.

Tackling the problem

Since this is a question about the prime factors of n, a good place to start might be to factorise n itself. We can see that n is a difference of two squares:

This can be factorised into:

So we now have the slightly easier problem of finding the prime factors of (p - 1) and (p + 1).

What can we tell about the factors?

What do we know about the two factors? There are two obvious things we can say:

• (p - 1) and (p + 1) differ by 2.

• (p - 1), p, and (p + 1) are consecutive.

Not forgetting, of course, we have been told that p is prime and greater than 3.

Finding the factors

Clearly at least one of (p - 1), p, and (p + 1) must be even, because they are consecutive.

But we know that p is a prime, and it isn't 2 (because it is greater than 3). This means that (p - 1) and (p + 1) must both be even.

So both factors are divisible by 2:

We can therefore say that n is divisible by 4.

But we can find out a bit more. Since (p - 1) is even we can write it as:

And since (p + 1) is 2 greater than (p - 1) we can write it as:

Now either k or k + 1 must be even. This means that exactly one of (p - 1) or (p + 1) must be divisible by 4 (the other is only divisible by 2).

So, n is not only divisible by 4, it is actually divisible by 8.

Another factor

That is not all, we can find another factor. Since (p - 1), p, and (p + 1) are consecutive, exactly one of those numbers must be divisible by 3. And we know that p cannot be divisible by 3, because it is a prime number greater than 3.

This means that exactly one of (p - 1) or (p + 1) must be divisible by 3. So, n is not only divisible by 8, it is also divisible by 3.

The result

This gives us the result that any number of the form:

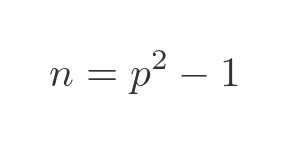
where p is a prime number greater than 3, is divisible by 24.

Let's check that

Let's try a few values.

5 squared is 25. Subtract 1 gives 24.

7 squared is 49. Subtract 1 gives 48 (2 times 24).

11 squared is 121. Subtract 1 gives 120 (5 times 24).

Let's try a bigger prime:

1237 squared is 1530169. Subtract 1 gives 1530168 (63757 times 24).

Did you figure it out?