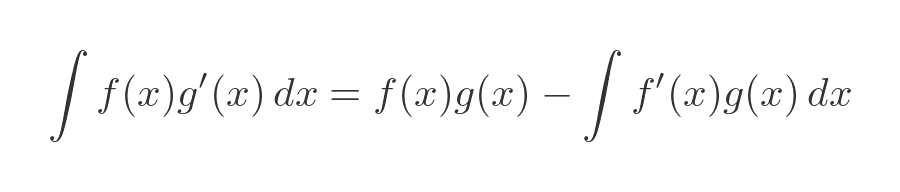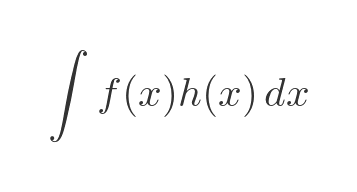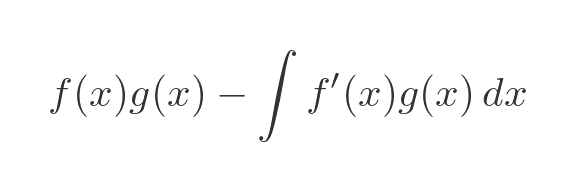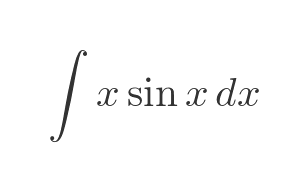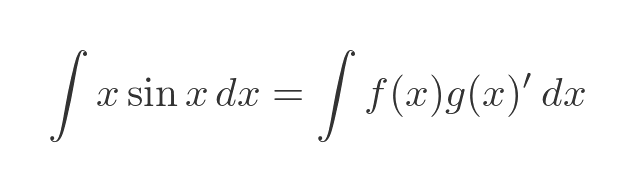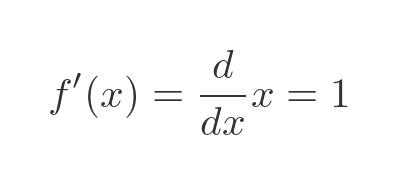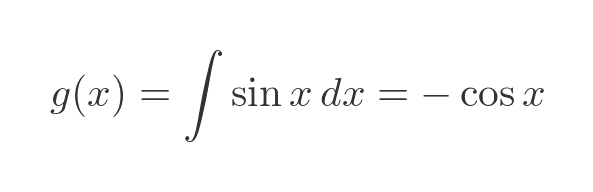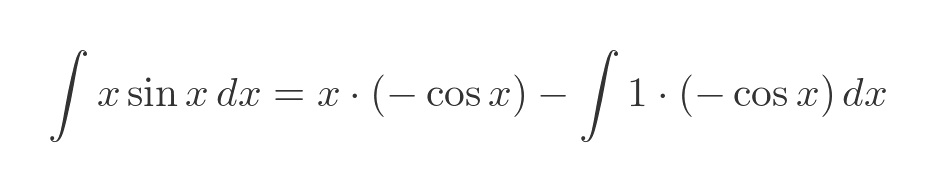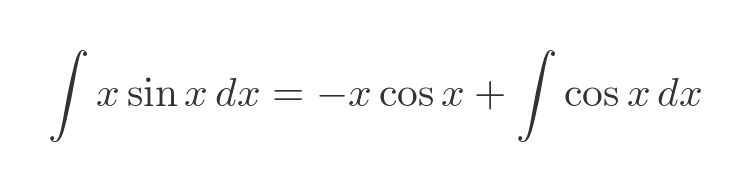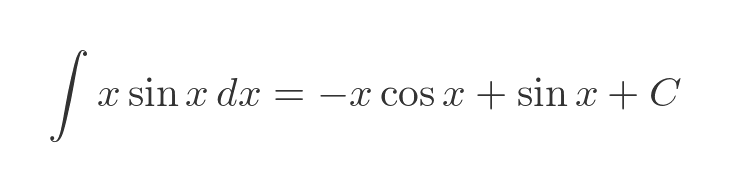Integration by parts

Finding integrals can be challenging because, unlike differentiation, we can't usually integrate a function from first principles. Instead, we usually find integrals by identifying a related differential equation and reversing it. For example, if we happen to know that the first derivative of the function f(x) is g(x), then (subject to a few conditions) we know that the integral of g(x) will be f(x).

This gives us a repertoire of standard integrals that we can use to solve problems. However, it is always useful to expand our repertoire. One way to do that is to investigate some of the rules we use for differentiating more complex expressions. These can sometimes be "reversed" to provide a new weapon in our integration armoury.

One well-known rule we use in differentiation is the product rule. The equivalent rule for integration is integration by parts. We will introduce that method in this article, with examples and a proof using calculus.

Integration by parts

Let's start by stating the rule as an indefinite integral (we will prove it later):

How is this useful? Well, suppose we have an expression to integrate but there is no known way to do it. But we notice that the expression is a factor of two other functions, like this:

Now suppose we happen to know that the integral of h is some other function g. In other words, h is equal to g'. So now we have this:

According to the formula above, we can rewrite this as:

This gives us a second chance at solving the integral. It might be that f' g is easier to integrate than f g'. This sometimes happens if f' is simpler than f. And since finding f(x) times g(x) is easy (it isn't under the integral sign) we have found a solution. This doesn't always work, but it sometimes does, so it is worth a try.

Let's look at a simple example:

We can't integrate this directly, so we will try integration by parts. We need to split the function into two factors, one that will represent f, and the other that will represent the derivative of some other function g:

Our function can be split into two factors fairly easily, it is x times sin x. Let's try defining f and g' like this:

We can now find f' by differentiating f:

We can find g by integrating g':

Looking back to the original rule:

We can substitute f, g and their derivatives:

Simplifying gives:

Evaluating the integral gives us the final result:

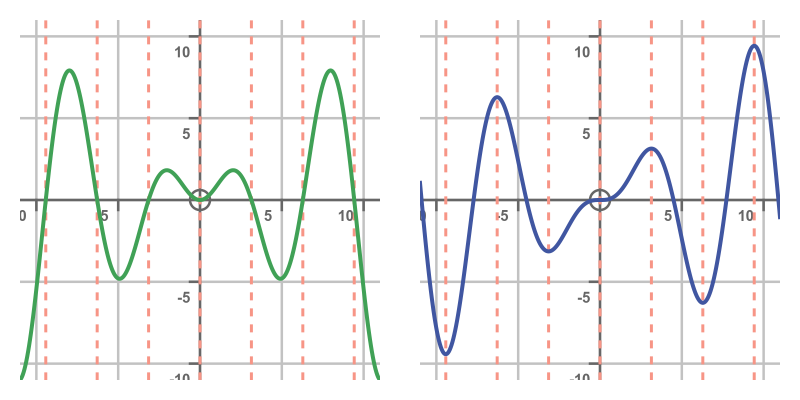
Here is a graph showing the original function on the left, and the integral on the right. As you would expect, the places where the left-hand graph is zero correspond to the turning points in the right-hand graph. Also, the regions where the left-hand graph is positive correspond to the regions where the right-hand graph has a positive slope, and vice versa. This gives us a small measure of confidence that the integral is correct:

Integration by parts doesn't always work

This technique is great when it works, but in many cases (in fact most cases) it won't work. As an example, consider what might happen if we had allocated f and g' differently. In this equation: