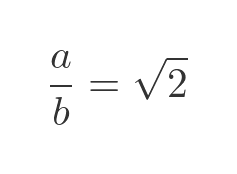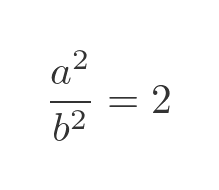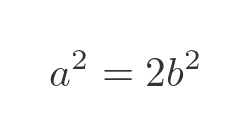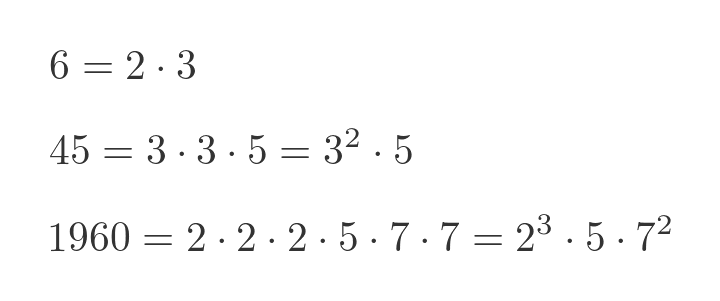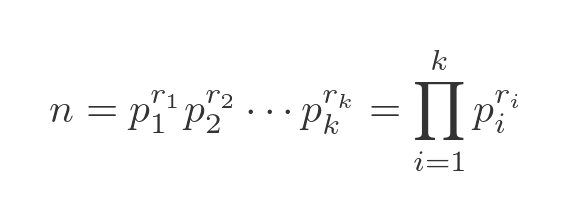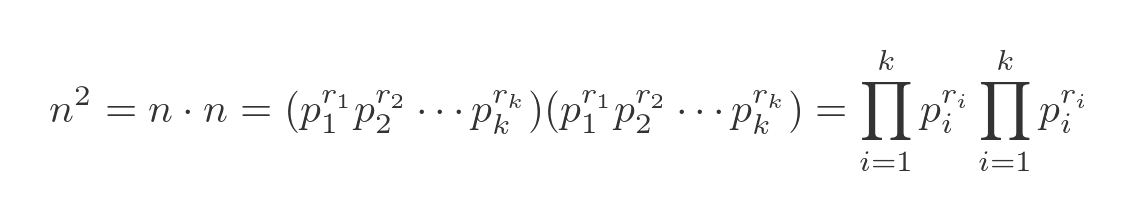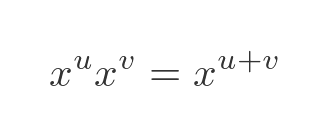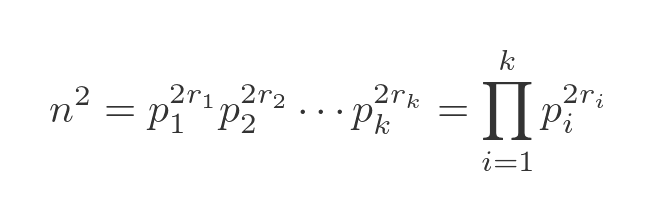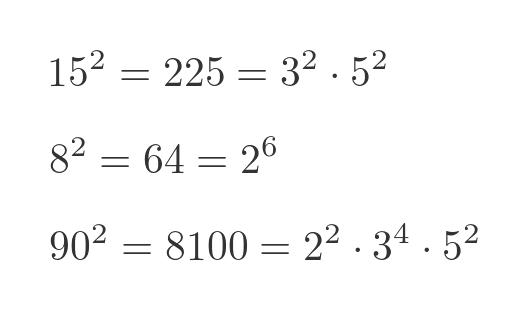Root 2 is irrational - proof by prime factors

There are several proofs that the square root of 2 is irrational. The earliest dates back to Euclid, around 300 BC. In this article, we will look at an alternative proof, based on prime factors.

This proof has several advantages:

• It is simpler.

• It can be easily applied to other numbers.

• It provides a good explanation of why perfect squares are a special case.

• It can be easily applied to higher powers.

• It can also be used to prove the stronger statement that any integer root of an integer value is either an integer or irrational.

Proof by contradiction

We will use a proof by contradiction. We will start by assuming that the square root of 2 is rational, and prove that this leads to a contradiction, so root 2 cannot be rational.

If root 2 was rational, then by definition, there must be some positive integers a and b for which:

Squaring both sides gives:

So for root 2 to be rational, there must be positive integer values a and b such that:

If we can prove that no such integer values can exist, then we have proved that the root of 2 cannot be rational and therefore must be irrational.

Prime factors

According to the fundamental theorem of arithmetic, every positive integer greater than 1 can be uniquely represented as a product of prime numbers. For example:

The theorem tells us two things. The first is that any positive number greater than 1 can be expressed as a product of one or more prime numbers. The second thing it tells us is that, for any particular number, there is only one way to do it. For instance, 45 can be expressed as 3 squared times 5, and there is no other way to express 45 as a product of primes.

The reason this only applies to numbers greater than 1 is that 1 itself is not a prime number.

For many numbers, the same prime number might appear as a factor more than once. For example, 1960 has three factors of 2, and two factors of 7. These can either be written as repeated multiplications or as powers (both are shown in the examples above). For this article, expressing them as powers is more useful, so we will use that notation from now on.

The number of times each prime appears in the factorisation is called the order of the factor. So in the example of 1960, we would say that 2 is a prime factor of order 3, 5 is a prime factor of order 1, and 7 is a prime factor of order 2. We could also say that 11 is a prime factor of order 0 because it doesn't appear in the factorisation at all.

In general, we can represent any integer n, greater than 1, as the product of a set of prime numbers p each raised to a positive integer power r:

Squaring a number using prime factors

The square of an integer n can be found by multiplying n by itself:

We can rearrange the product, by grouping each pair of factors for each prime:

Now we know from basic arithmetic that when we multiply powers of the same base, we just add the exponents:

In our case, the exponents are equal, so we get this:

So to calculate n squared, we take the prime factors of n and double each of the powers. But the really important thing we get from this is that for a perfect square, the exponent of every prime factor is an even number. For example:

Proof that the square root of 2 is irrational