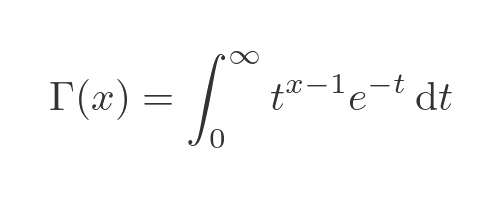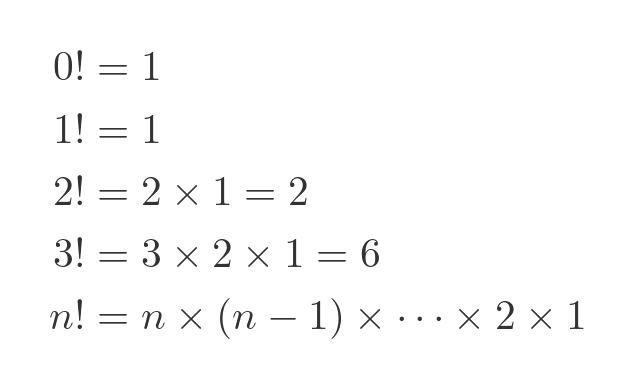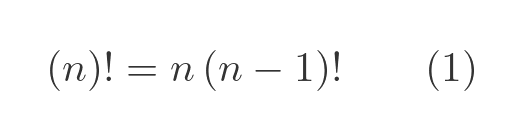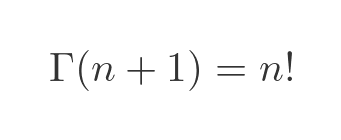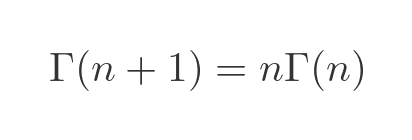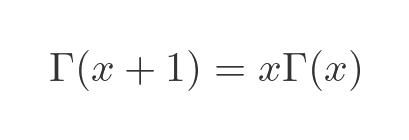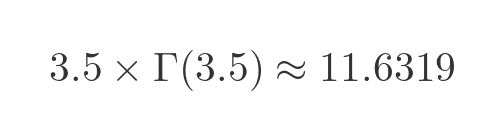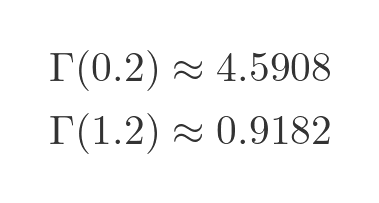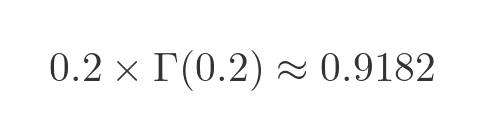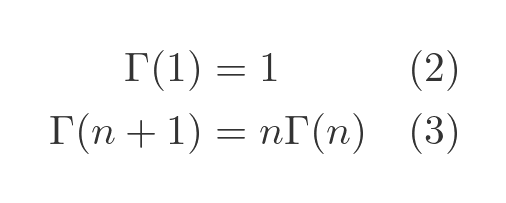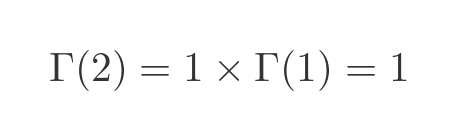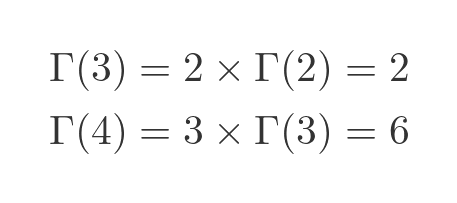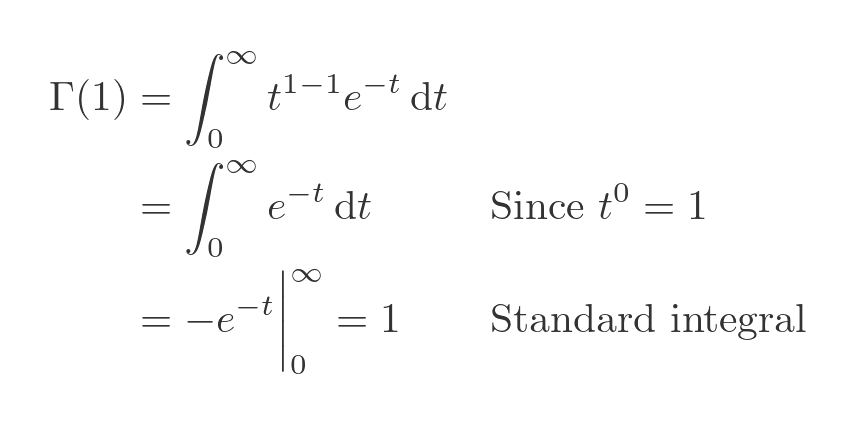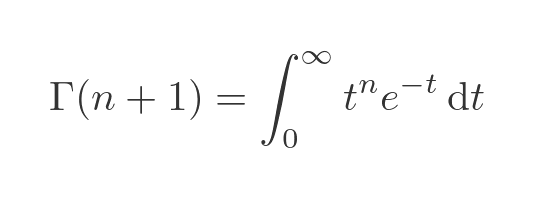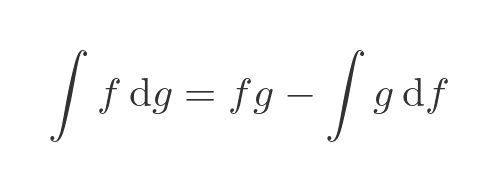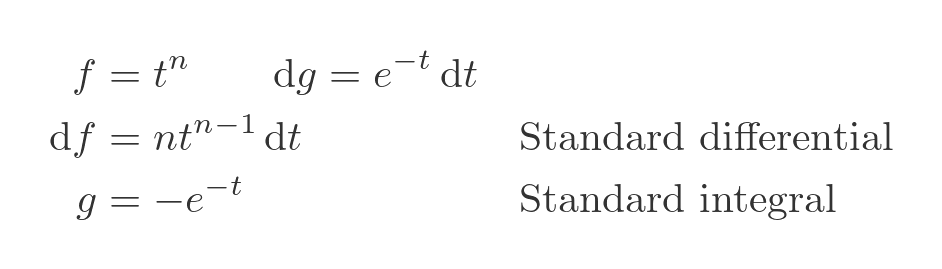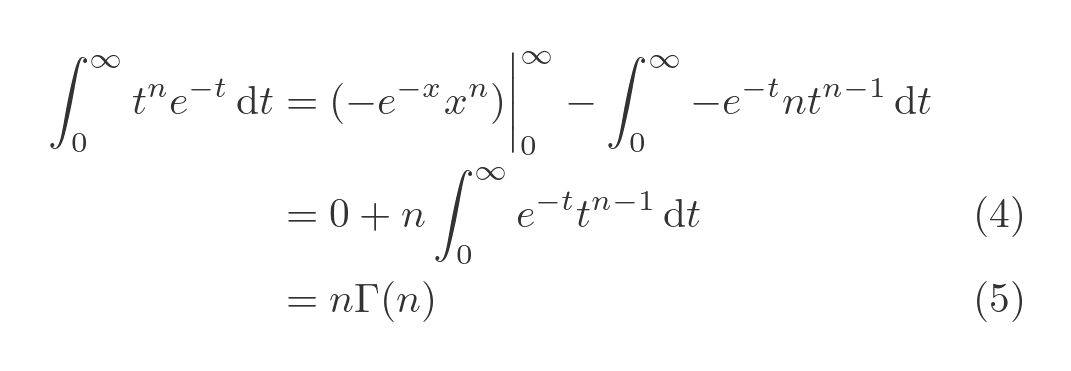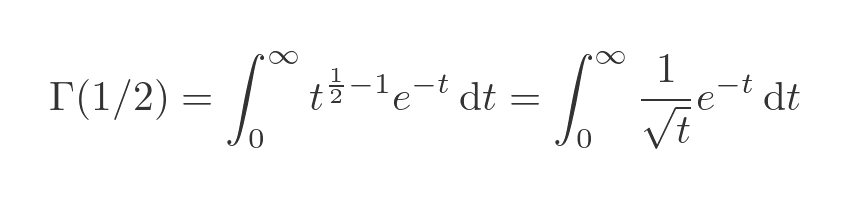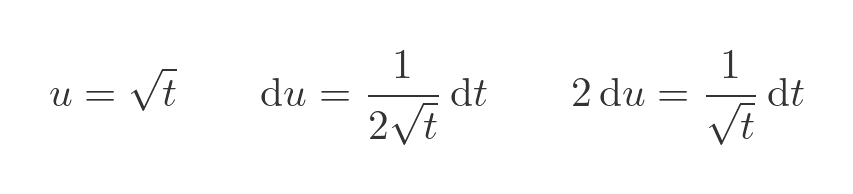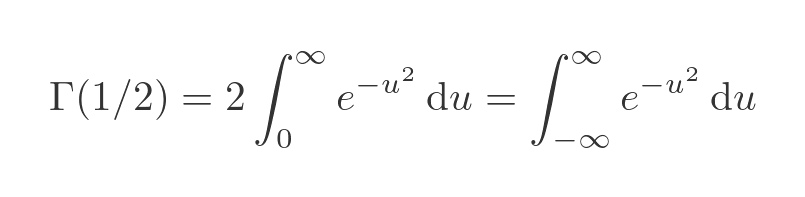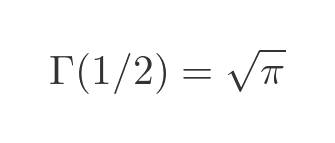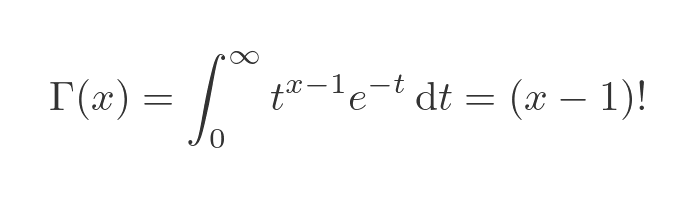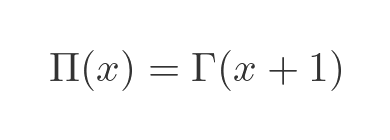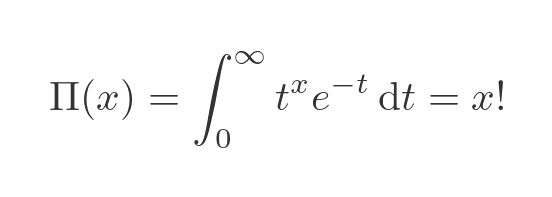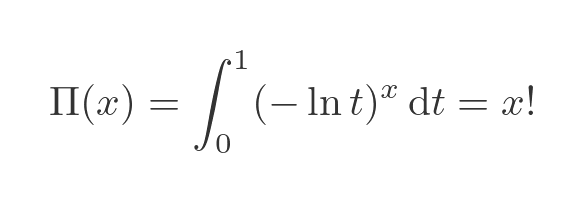The gamma function

The gamma function, Γ(x), is a special function that has several uses in mathematics, including solving certain types of integration problems, and some important applications in statistics.

The function also allows us to extend the idea of a factorial to non-integer values, so we can (sort of) find the factorial of 1/2, or π. That is the area we will mainly concentrate on in this article.

Definition of the gamma function

Before we look at the properties of the gamma function, let's look at its definition. It is actually defined by an integral:

Notice that this is a function of x, not a function of t. t is the variable of integration, but the function being integrated depends on x. So the value of the function depends only on x, not t.

This integral has no solution in terms of standard functions, but we can calculate its approximate value to many decimal places.

Factorials

The factorial function n!, is defined for non-negative integers as:

The essential property of factorials is that, for integer n > 0:

Remember, of course, that 0! is equal to 1.

The gamma function

The gamma function Γ has the property that, for any integer n > 0:

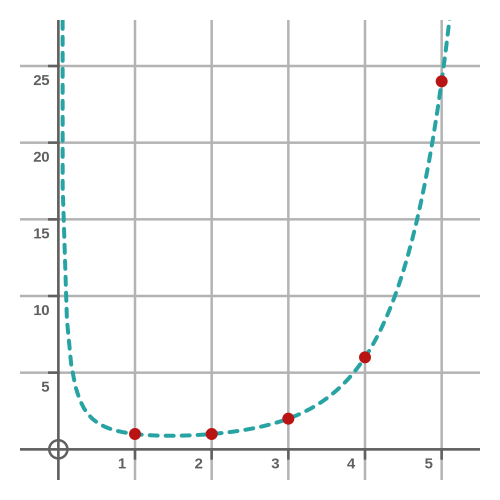
That means that the function passes through the points (1, 0!), (2, 1!), (3, 2!) and so on. Those points are plotted on the graph below:

The dashed curve shows the gamma function. The curve interpolates the points smoothly. But why does it increase as x approaches zero?

A second feature of the gamma function

Since the values of the gamma function for integer n > 0 are factorials, then it is also true that:

This follows from the equivalent formula for factorials, equation (1) above. It turns out that this formula above doesn't only apply to integers, it applies to all values of x:

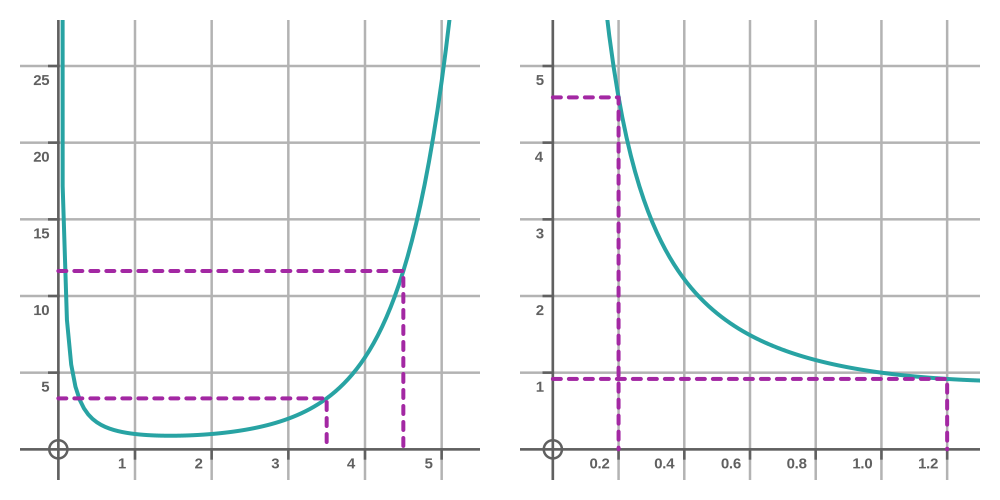
These graphs show a couple of examples:

The LHS shows the case when x is 3.5. In that case, we have:

As mentioned earlier, although we cannot solve the gamma function integral exactly, we can calculate its approximate value to many decimal places. We are using 4 places here to validate that the factorial rule applies (we will prove it later). If we multiply Γ(3.5) by 3.5 we get Γ(4.5) (to within 4 places) as expected:

The RHS of the graph shows the same calculation when x is 0.2:

Again, Γ(0.2) by 0.2 gives Γ(1.2):

This also explains why the gamma function gets large as x becomes very small:

• For some very small value ε, the value of 1 + ε is close to 1.

• Since Γ(1) is 1, it means that Γ(1 + ε) is close to 1.

• Since εΓ(ε) = Γ(1 + ε) ≈ 1, it follows that Γ(ε) must get very large as ε gets very small (because their product is 1).

Proof Γ(n + 1) is n!

We can prove that Γ(n + 1) is n!, for integer n > 0. We will use induction. We just need to prove the following:

Starting with equation (2), applying (3) gives us:

Applying (3) again and again gives:

And so on.

Statement (2) can be proved quite easily. For brevity, we will assume some standard results. We simply substitute x = 1 into gamma function definition from earlier:

To prove (3), we again start from the definitions of the gamma function, this time for n + 1:

We will use integration by parts. As a reminder, here is the standard equation for integration by parts:

We will use the following values for f and dg, and obtain df and g by differentiating and integrating. They are standard results:

Putting these values back into the original equation gives:

On the first line is just the integration by parts formula, with all our values substituted in.

In equation (4), we notice that the first term (fg in the integration by parts formula) goes to zero. That is because, when x is zero, the exponential term is 1 and the x^n term is zero, so the whole thing is zero. When x goes to infinity, the term is also zero. That is because the exponential term goes to zero. The x^n term goes to infinity, but the exponential term falls faster than the power term rises, so overall it goes to zero. We won't prove that here, but it can be shown fairly easily using L'Hôpital's rule.

We also tidy up the integral term. In (5), we notice that the integral term is equal to nΓ(n), so Γ(n + 1) = nΓ(n), which completes our proof.

Gamma function for fractional values

Now we will take a quick look at how we can calculate the gamma function for a fractional value. We will use the value of 1/2 because it gives quite a nice result. We use the standard gamma function definition, with a value of 1/2:

We used the fact that t to the power -1/2, of course, is one over root t. We can now do a change of variables to turn the square root into something a bit nicer:

Substituting this into the integral gives:

Here we have used the fact that the function we are integrating is a function of u squared, so it is symmetrical about x = 0. This means that the integral from 0 to infinity is exactly half the integral from minus infinity to infinity. That transformation means that the integral now takes the exact form the famous Gaussian integral. This integral is known to evaluate to the square root of pi. So:

The pi function

One slightly messy thing about the gamma function is that Γ(x) returns the factorial of x - 1. There is also a slightly ugly x - 1 term inside the integral:

What if we had a different function that returned x! directly? Well, actually, there is such a function, called the pi function. It is defined like this:

Here is what happens when we calculate Π(x):

This is much neater. It calculates x! directly, and the integral is a bit cleaner. And not only that, but the pi function was discovered before the gamma function. So why is everyone taught the gamma function, but hardly anyone has even heard of the pi function?

Unfortunately, there is no good answer to that question. The gamma function is slightly better for certain calculations, but often the pi function is simpler. There are a couple of speculative reasons that may ot may not have anything to do with it. The first is that the pi function was originally developed in this form:

This is quite a lot messier than the gamma function form, although it can be transformed into that form by a simple change of variables.

Another possible reason is that capital Π is often used to signify a product series, so having a function called Π is potentially misleading. But we will probably never know.